Phénomène de Gibbs

Soit $f:\mathbb R \to \mathbb R$ la fonction $2\pi$-périodique définie sur $[-\pi,\pi[$ par
$f(x)=\begin{cases} 1,& x \in [-\frac{\pi}2,\frac{\pi}2]\\ 0,& x \in [-\pi, \frac{\pi}2[ \cup]\frac\pi2,\pi[. \end{cases}$

Vu qu’il s’agit d’une fonction paire, les coefficients de Fourier $b_n$ seront nuls.
On a
$a_n=\frac{1}\pi\int_{-\pi}^\pi f(x)\cos(nx)\, dx = \frac1\pi \int_{-\pi/2}^{\pi/2} \cos(nx)\, dx=\frac{2\sin(\frac\pi2 n)}{\pi n}$
si $n>0$ et $a_0=1$.
D’après le théorème de Dirichlet la série de Fourier converge simplement vers la régularisée de $f$.
C’est à dire
$\frac{a_0}2+ \sum_{n=1}^\infty a_n \cos(n x) = f(x)$
si $x \in [-\pi,\pi]\setminus \{-\frac{\pi}{2},\frac{\pi}{2}\}$.
Par contre la convergence ne peut pas etre uniforme sur $[-\pi,\pi]$ car sinon la limite serait une fonction continue.
Donc il existe un $\varepsilon>$ tel que pour tout $n_0 \in \mathbb N$ il existe $n\geq n_0$ et $x_n \in [-\pi,\pi]$ tel que $|f(x_n)-\sum_{k=0}^n a_k\cos(k x)|\geq \varepsilon$.

Sur les images suivants on voit la fonction $f$ en rouge et les sommes partielles de rangs 1, 3, 7, 19, 49 et 70 de la série de Fourier en bleu. On peut observer le comportement décrit ci-dessus.

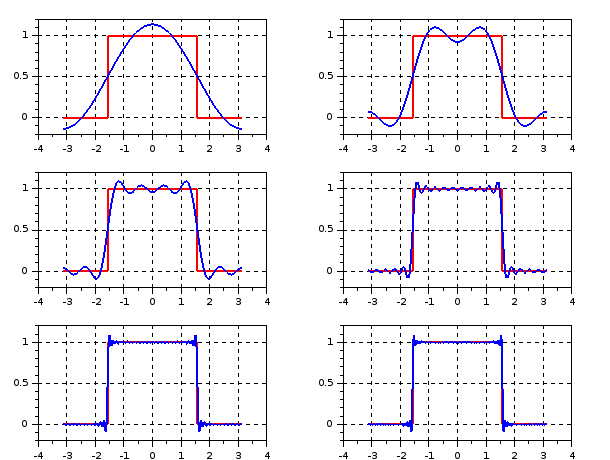
De plus, une fois qu’on voit les images, il semble que

1. Le $\varepsilon$ ci-dessus est relativement large.
2. Le $n$ qui existe pour tout $n_0$ est de la forme $n=n_0$.

Ces deux observations expérimentales peuvent être prouvées rigoureusement (ce qu’on ne fera pas ici).
Exercice 1
a) Écrire un script, qui produira des images comme celui ci-dessus.
Indication : les commandes suivantes seront utiles: linspace, ones, clf, subplot, plot, xgrid (écrire par exemple help linspace pour voir leur descriptif).
Le script commencera comme suit :

t=linspace(-%pi,%pi,2000);
sq=[zeros(1,500),ones(1,1000),zeros(1,500)];
N=[1,3,7,19,49,70];
clf();

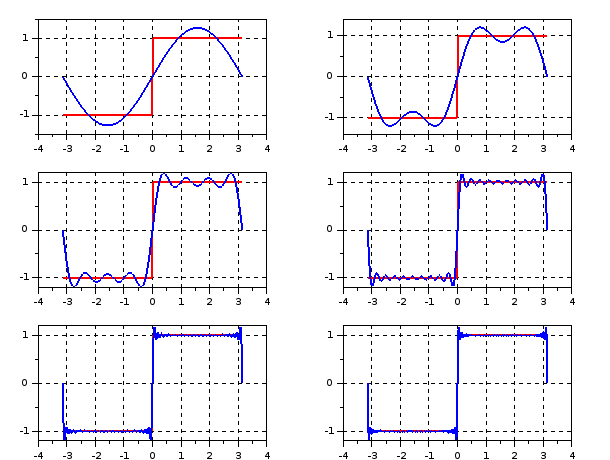
b) Faire le même pour la fonction $f(x)=\text{sign}(x)$ sur $[-\pi,\pi]$

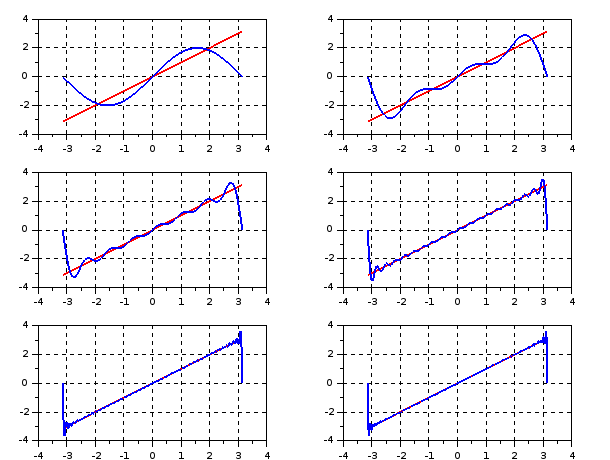
c) Et pour la fonction $f(x)=x$ sur $[-\pi,\pi]$.

Phénomène de Gibbs et transformée de Fourier discrète

Maintenant, on va essayer d’écrire un script qui va faire les calculs automatiquement pour toute fonction donnée.
D’abord il faut s’expliquer comment on peut calculer la transformée de Fourier d’une fonction quelconque dans SciLab. La transformée de Fourier discrète est idéale pour ce but.

Définition Soit $N \in \mathbb N$. Si $f \in \mathbb C^N$ alors
$Df(k)=\sum_{n=0}^{N-1}f(n)\exp(-i\frac{2\pi}{N}kn),\, k\in \mathbb Z$
s’appelle la transformée de Fourier discrète de $f$ (TFD).

Il est clair que cette suite est $N$-periodique (c’est à dire $Df(k+N)=Df(k)$ pour tout $k \in \mathbb Z$) et on peut donc considérer que $Df \in \mathbb C^N$.

Dans SciLab la TFD de $f$ se obtient en utilisant fft(f,-1).
Il faut faire attention aux indices car si x=fft(f,-1) alors $x(1)=Df(0)$ et $x(N)=Df(N-1)$.

Faisons un exemple :

S=[zeros(1,500),ones(1,1000),zeros(1,500)];
y=fft(S);
clf()
subplot(1,3,1);
plot(S,'r','LineWidth',2);
subplot(1,3,2);
plot(real(y),'b','LineWidth',2);
subplot(1,3,3);
plot(imag(y),'b','LineWidth',1);

Proposition L’application $D:\mathbb C^N \to \mathbb C^N$ est bijective.
Sa réciproque est
$D^{-1}f(k)=\frac{1}{N}\sum_{n=0}^{N-1}f(n)\exp(i\frac{2\pi}{N}kn).$

Dans SciLab la TFD inverse de $f$ se obtient en utilisant fft(f,1).
Attention, dans le help fft il y a un erreur dans la description mathématique de la fft(f,1) (oubli de diviser par $N$).

Mais pour notre but nous avons besoin de sommes partielles de la série de Fourier.
Traitons pour l’instant les coefficients de $(Df(k))_{k\in \mathbb Z}$ comme les véritables coefficients de Fourier.
Dans ce cas les sommes partielles seront:
$S_m(k)=\frac1N\sum_{n=-m}^{m}Df(n)\exp(i\frac{2\pi}{N}kn)$
$=Df(0)+\sum_{n=1}^m\left(Df(n)\exp(i\frac{2\pi}{N}kn)+Df(-n)\exp(-i\frac{2\pi}{N}kn) \right)$
$=Df(0)+\sum_{n=1}^m\left(Df(n)\exp(i\frac{2\pi}{N}kn)+Df(N-n)\exp(-i\frac{2\pi}{N}kn) \right)$
où on a utilisé le fait que $Df$ est $N$-periodique.
Exercice 2
Finir d’écrire le script suivant dans le but de calculer et afficher les sommes partielles de la série de Fourier de la fonction S ci-dessous.

t=1:2000;//linspace(-%pi,%pi,2000);
S=[zeros(1,500),ones(1,1000),zeros(1,500)];
y=fft(S);
N=[1,3,7,19,49,999];
clf();

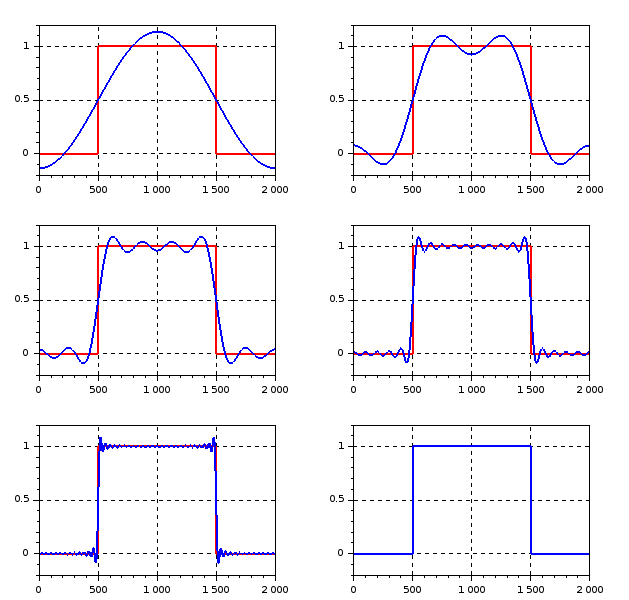
Ce qu’on voit est qu’on arrive reproduire le phénomène de Gibbs pour les petites valeurs de $m$ tandis qu’il disparaît pour les grandes valeurs proches de $N/2$.
Ceci ne devrait pas être une grande surprise car nous avons déjà dit que $D:\mathbb C^N \to \mathbb C^N$ est bijective, donc si on utilise tous les coefficients $(Df(k))_{k=0}^{N-1}$ on peut récupérer la suite $(f(n))_{n=0}^{N-1}$ complètement.
Dans la première partie de ce TP nous avons manuellement calculées les coefficients de Fourier de la véritable fonction $f:\mathbb R \to \mathbb R$ (supposée $2\pi$-periodique), ici nous avons accès seulement à un nombre fini de valeurs de cette fonction.
Il se trouve que les coefficients $Df(k)$ sont seulement une approximation (à une constante multiplicative près) des coefficients de Fourier $c_k(f)$. En effet, on a
$c_k(f)=\frac{1}{2\pi}\int_0^{2\pi} f(t)\exp(-ikt)\, dt \approx$
$\approx \frac{1}{N}\sum_{n=0}^{N-1} f(\frac{n2\pi}{N})\exp(-i\frac{kn2\pi}{N})=\frac1NDf(k)$
C’est l’approximation par une somme de Riemann. On voit qu’à $N$ fixé, elle n’est pas précise pour grandes valeurs de $|k|$ (car, par exemple, $Df$ est $N$-periodique et $\lim c_k(f)=0$) .

Remarque La fonction fft de SciLab utilise pour trouver la TFD de $f$ un algorithme appelé la transformé de Fourier rapide.
Cet algorithme se base (dans le cas $N=2^k$) sur une décomposition dyadique du produit matriciel caché dans la définition de $Df$.
Il permet de réduire le nombre d’opérations arithmétiques nécessaires pour le calcul de $Df$ : $O(N\log_2(N))$ au lieu de $O(N^2)$.
Cet algorithme améliore aussi la précision numérique du calcul.
Voir help fft pour un comparaison de la vitesse et précision du calcul.

Written with StackEdit.